Triangular Numbers

The first ten triangular numbers are –
1, 3, 6, 10, 15, 21, 28, 36, 45, 55

You can calculate triangular numbers by adding up consecutive numbers. For example, the eighth triangular number is equal to –
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8
– which comes to 36.

As the name suggests, you can visualise triangular numbers as a triangle of points.

Everyone in a group of people shakes hands with everyone else. The total number of handshakes will always be a triangular number. For instance, five people will make ten handshakes.

There is a useful short cut if you want to work out a large triangular number. Suppose you want the 100th triangular number. You could add up all the numbers from 1 to 100. But there is a simpler way. First work out the average number by adding together the first and the last number, and dividing by two –
1 + 100 = 101
101 / 2 = 50.5

Now multiply this average by however many numbers you would have to add up, in this case, by 100 –
50.5 × 100 = 5050
– so the 100th triangular number is 5050.

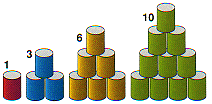
The first four triangular numbers. How many do you have to add each time?

Based on the book Numbers: Facts, Figures & Fiction.